TI-BASIC:Rref
Command Summary
Puts a matrix into reduced row-echelon form.
Command Syntax
rref(matrix)
Menu Location
Press:
- MATRX (on the TI-83) or 2nd MATRX (TI-83+ or higher) to access the matrix menu.
- RIGHT to access the math menu.
- ALPHA B to select rref(, or use arrows and ENTER.
TI-83/84/+/SE
2 bytes
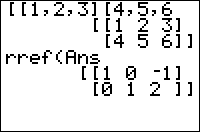
Given a matrix with at least as many columns as rows, the rref( command puts a matrix into reduced row-echelon form using Gaussian elimination.
This means that as many columns of the result as possible will contain a pivot entry of 1, with all entries in the same column, or to the left of the pivot, being 0.
[[1,2,5,0][2,2,1,2][3,4,6,2]] [[1 2 5 0] [2 2 1 2] [3 4 7 3]] rref(Ans) [[1 0 0 6 ] [0 1 0 -5.5] [0 0 1 1 ]]
Advanced Uses
The rref( command can be used to solve a system of linear equations. First, take each equation, in the standard form of <math>\definecolor{darkgreen}{rgb}{0.90,0.91,0.859}\pagecolor{darkgreen}a_1x_1+\dots + a_nx_n = b</math>, and put the coefficients into a row of the matrix.
Then, use rref( on the matrix. There are three possibilities now:
- If the system is solvable, the left part of the result will look like the identity matrix. Then, the final column of the matrix will contain the values of the variables.
- If the system is inconsistent, and has no solution, then it will end with rows that are all 0 except for the last entry.
- If the system has infinitely many solutions, it will end with rows that are all 0, including the last entry.
This process can be done by a program fairly easily. However, unless you're certain that the system will always have a unique solution, you should check that the result is in the correct form, before taking the values in the last column as your solution. The Matr►list( command can be used to store this column to a list.
Error Conditions
- ERR:INVALID DIM is thrown if the matrix has more rows than columns.
Related Commands
- Ref(
- |- and other row operations.