TI-BASIC:Invnorm
Command Summary
Calculates the inverse of the cumulative normal distribution function.
Command Syntax
invNorm(probability[,μ, σ])
Menu Location
Press:
- 2ND DISTR to access the distribution menu
- 3 to select invNorm(, or use arrows.
TI-83/84/+/SE
2 bytes
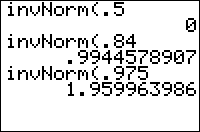
invNorm( is the inverse of the cumulative normal distribution function: given a probability, it will give you a z-score with that tail probability. The probability argument of invNorm( is between 0 and 1; 0 will give -1E99 instead of negative infinity, and 1 will give 1E99 instead of positive infinity
There are two ways to use invNorm(. With three arguments, the inverse of the cumulative normal distribution for a probability with specified mean and standard deviation is calculated. With one argument, the standard normal distribution is assumed (zero mean and unit standard deviation). For example:
for the standard normal distribution :invNorm(.975 for the normal distribution with mean 10 and std. dev. 2.5 :invNorm(.975,10,2.5
Advanced
This is the only inverse of a probability distribution function available (at least on the TI 83/+/SE calculators), so it makes sense to use it as an approximation for other distributions. Since the normal distribution is a good approximation for a binomial distribution with many trials, we can use invNorm( as an approximation for the nonexistent "invBinom(". The following code gives the number of trials out of N that will succeed with probability X if the probability of any trial succeeding is P (rounded to the nearest whole number):
:int(.5+invNorm(X,NP,√(NP(1-P
You can also use invNorm() to approximate the inverse of a t-distribution. Since a normal distribution is a t-distribution with infinite degrees of freedom, this will be an overestimate for probabilities below 1/2, and an underestimate for probabilities above 1/2.
Formulas
Unlike the Normalpdf( and Normalcdf( commands, the invNorm( command does not have a closed-form formula. It can however be expressed in terms of the [wikipedia:Error_function inverse error function]: Template:TI-BASIC:Math
For the arbitrary normal distribution with mean μ and standard deviation σ: Template:TI-BASIC:Math