Difference between revisions of "TI-BASIC:Angle"
(Initial automated import) |
Battlesquid (talk | contribs) |
||
| Line 12: | Line 12: | ||
angle(''z'') returns the [http://mathworld.wolfram.com/ComplexArgument.html complex argument] (also known as the polar angle) of the complex number ''z''. If ''z'' is represented as ''x''+i''y'' where ''x'' and ''y'' are both real, angle(''z'') returns R►Pθ(''x'',''y'') (which is equivalent to tanֿ¹(''y''/''x'') if x is nonzero). Also works on a list of complex numbers. | angle(''z'') returns the [http://mathworld.wolfram.com/ComplexArgument.html complex argument] (also known as the polar angle) of the complex number ''z''. If ''z'' is represented as ''x''+i''y'' where ''x'' and ''y'' are both real, angle(''z'') returns R►Pθ(''x'',''y'') (which is equivalent to tanֿ¹(''y''/''x'') if x is nonzero). Also works on a list of complex numbers. | ||
| − | + | <div style="background: #FFF; border: 1px dashed #DDD; padding-left:1em; margin: 1em 0 1em 0; font-family:Arial Unicode MS; color: #000; letter-spacing:1.2pt;"> | |
angle(3+4i) | angle(3+4i) | ||
.927295218 | .927295218 | ||
R►Pθ(3,4) | R►Pθ(3,4) | ||
.927295218 | .927295218 | ||
| − | + | </div> | |
When writing a complex number ''z'' in the form <math>re^{i\theta}</math> (or, equivalently, <math>r(\cos\theta+i\sin\theta)</math>), then <math>\theta</math> is equal to the value of angle(''z''), suitably reduced so that the result returned is in the interval <math>-\pi<\theta\leq\pi</math>. | When writing a complex number ''z'' in the form <math>re^{i\theta}</math> (or, equivalently, <math>r(\cos\theta+i\sin\theta)</math>), then <math>\theta</math> is equal to the value of angle(''z''), suitably reduced so that the result returned is in the interval <math>-\pi<\theta\leq\pi</math>. | ||
Latest revision as of 02:33, 27 November 2017
Command Summary
Returns the complex argument of a complex number.
Command Syntax
angle(z)
Menu Location
Press:
- MATH to access the Math menu.
- RIGHT, RIGHT to access the CPX (complex) submenu
- 4 to select angle(, or use arrows.
TI-83/84/+/SE
2 bytes
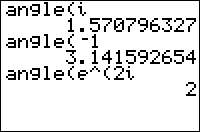
angle(z) returns the complex argument (also known as the polar angle) of the complex number z. If z is represented as x+iy where x and y are both real, angle(z) returns R►Pθ(x,y) (which is equivalent to tanֿ¹(y/x) if x is nonzero). Also works on a list of complex numbers.
angle(3+4i)
.927295218
R►Pθ(3,4)
.927295218
When writing a complex number z in the form <math>re^{i\theta}</math> (or, equivalently, <math>r(\cos\theta+i\sin\theta)</math>), then <math>\theta</math> is equal to the value of angle(z), suitably reduced so that the result returned is in the interval <math>-\pi<\theta\leq\pi</math>.
The angle( command also works on Matrices, though not in any useful way: angle([A] will return a matrix of the same size as [A], but with all elements 0. If you plan to use this, don't: 0[A] does the same thing, but is smaller and not as questionable (because this behavior is clearly unintentional on TI's part, and may be changed in an OS update).