TI-BASIC:Rref

Command Summary

Puts a matrix into reduced row-echelon form.

Command Syntax

rref(matrix)

Menu Location

Press:

1. MATRX (on the TI-83) or 2nd MATRX (TI-83+ or higher) to access the matrix menu.
2. RIGHT to access the math menu.
3. ALPHA B to select rref(, or use arrows and ENTER.

Calculator Compatibility

TI-83/84/+/SE

Token Size

2 bytes

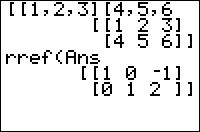
Given a matrix with at least as many columns as rows, the rref( command puts a matrix into reduced row-echelon form using Gaussian elimination.

This means that as many columns of the result as possible will contain a pivot entry of 1, with all entries in the same column, or to the left of the pivot, being 0.

[[1,2,5,0][2,2,1,2][3,4,6,2]]
	[[1 2 5 0]
	 [2 2 1 2]
	 [3 4 7 3]]
rref(Ans)
	[[1 0 0 6   ]
	 [0 1 0 -5.5]
	 [0 0 1 1   ]]

Advanced Uses

The rref( command can be used to solve a system of linear equations. First, take each equation, in the standard form of <math>\definecolor{darkgreen}{rgb}{0.90,0.91,0.859}\pagecolor{darkgreen}a_1x_1+\dots + a_nx_n = b</math>, and put the coefficients into a row of the matrix.

Then, use rref( on the matrix. There are three possibilities now:

• If the system is solvable, the left part of the result will look like the identity matrix. Then, the final column of the matrix will contain the values of the variables.
• If the system is inconsistent, and has no solution, then it will end with rows that are all 0 except for the last entry.
• If the system has infinitely many solutions, it will end with rows that are all 0, including the last entry.

This process can be done by a program fairly easily. However, unless you're certain that the system will always have a unique solution, you should check that the result is in the correct form, before taking the values in the last column as your solution. The Matr►list( command can be used to store this column to a list.

Error Conditions

• ERR:INVALID DIM is thrown if the matrix has more rows than columns.

Related Commands

• Ref(
• |- and other row operations.