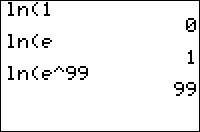TI-BASIC:Ln: Difference between revisions
Initial automated import |
KermMartian (talk | contribs) No edit summary |
||
| Line 15: | Line 15: | ||
Using either the ln( or the [[TI-BASIC:Log|Log(]] command, logarithms of any base can be calculated, using the identity: | Using either the ln( or the [[TI-BASIC:Log|Log(]] command, logarithms of any base can be calculated, using the identity: | ||
<math> | |||
\log_b{x} = \frac{\ln{x}}{\ln{b}} = \frac{\log{x}}{\log{b}} | \log_b{x} = \frac{\ln{x}}{\ln{b}} = \frac{\log{x}}{\log{b}} | ||
</math> | |||
So, to take the base B log of a number X, you could use either of the following equivalent ways: | So, to take the base B log of a number X, you could use either of the following equivalent ways: | ||
| Line 37: | Line 37: | ||
* ''[[TI-BASIC:E_Exponent|e^(]]'' | * ''[[TI-BASIC:E_Exponent|e^(]]'' | ||
* [[TI-BASIC:Log|Log(]] | * [[TI-BASIC:Log|Log(]] | ||
* [[TI-BASIC:Logbase|LogBASE(]][[Category:TI-BASIC]] | * [[TI-BASIC:Logbase|LogBASE(]] | ||
[[Category:TI-BASIC]] | |||
[[Category:TIBD]] | [[Category:TIBD]] | ||
Latest revision as of 19:15, 24 February 2016
Command Summary
Computes the (principal branch of the) natural logarithm.
Command Syntax
ln(value)
Menu Location
Press the LN key to paste ln(.
TI-83/84/+/SE
1 byte
The ln( command computes the natural logarithm of a value -- the exponent to which the constant e must be raised, to get that value. This makes it the inverse of the e^( command.
ln( is a real number for all positive real values. For negative numbers, ln( is an imaginary number (so taking ln( of a negative number will cause ERR:NONREAL ANS to be thrown in Real mode), and of course it's a complex number for complex values. ln( is not defined at 0, even if you're in a complex mode.
Advanced Uses
Using either the ln( or the Log( command, logarithms of any base can be calculated, using the identity: <math> \log_b{x} = \frac{\ln{x}}{\ln{b}} = \frac{\log{x}}{\log{b}} </math>
So, to take the base B log of a number X, you could use either of the following equivalent ways:
:log(X)/log(B)
:ln(X)/ln(B)
This is the exponent to which B must be raised, to get X.
Error Conditions
- ERR:DOMAIN when calculating ln(0).
- ERR:NONREAL ANS if taking ln( of a negative number in Real mode.