TI-BASIC:E Exponent: Difference between revisions
Initial automated import |
Automated superscript correction |
||
| (One intermediate revision by one other user not shown) | |||
| Line 3: | Line 3: | ||
|summary=Raises the constant ''e'' to the ''value'' power. | |summary=Raises the constant ''e'' to the ''value'' power. | ||
|syntax=''e''^(''value'') | |syntax=''e''^(''value'') | ||
|location=Press [2nd] [''e'' | |location=Press [2nd] [''e''<sup>x</sup>] to paste ''e''^(. | ||
|compatibility=TI-83/84/+/SE | |compatibility=TI-83/84/+/SE | ||
|size=1 byte | |size=1 byte | ||
| Line 25: | Line 25: | ||
The ''e''^( is usually defined by an infinite series: | The ''e''^( is usually defined by an infinite series: | ||
<math> | |||
e^x=\sum_{n=0}^\infty{\frac{x^n}{n!}} | e^x=\sum_{n=0}^\infty{\frac{x^n}{n!}} | ||
</math> | |||
This is then used to define exponentiation in general (for all real and even complex numbers), rather than using some sort of definition of exponents that involves multiplying a number by itself many times (which only works for integers). | This is then used to define exponentiation in general (for all real and even complex numbers), rather than using some sort of definition of exponents that involves multiplying a number by itself many times (which only works for integers). | ||
Latest revision as of 22:24, 24 February 2016
Command Summary
Raises the constant e to the value power.
Command Syntax
e^(value)
Menu Location
Press [2nd] [ex] to paste e^(.
TI-83/84/+/SE
1 byte
The e^( command raises the constant e to a power. Since it's possible to just type out e, ^, and (, the reason for having a separate function isn't immediately obvious, but in fact most of the time you need to use e, it's to raise it to a power.
The trigonometric and hyperbolic functions can be expressed, and in fact are usually defined, in terms of e^(.
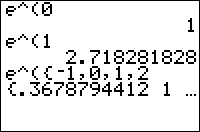
e^( accepts numbers and lists (but unfortunately not matrices) as arguments. It also works, and is often used for, complex numbers (in fact, one of the standard forms of complex numbers on TI-83 series calculators is re^θi, which uses the e^( function)
e^(2)
7.389056099
e^(πi)
-1
e^({-1,0,1})
{.3678794412 1 2.718281828}
Formulas
The e^( is usually defined by an infinite series:
<math> e^x=\sum_{n=0}^\infty{\frac{x^n}{n!}} </math>
This is then used to define exponentiation in general (for all real and even complex numbers), rather than using some sort of definition of exponents that involves multiplying a number by itself many times (which only works for integers).