TI-BASIC:Tanh: Difference between revisions
Initial automated import |
KermMartian (talk | contribs) No edit summary |
||
| Line 24: | Line 24: | ||
The tanh( command can be used to approximate the sign function: | The tanh( command can be used to approximate the sign function: | ||
<math> | |||
\operatorname{sgn} x=\begin{cases}-1&\text{if }x<0,\\0&\text{if }x=0,\\1&\text{if }x>0.\end{cases} | \operatorname{sgn} x=\begin{cases}-1&\text{if }x<0,\\0&\text{if }x=0,\\1&\text{if }x>0.\end{cases} | ||
</math> | |||
As the absolute value of the input becomes large, the convergence is achieved at a point closer to zero. For the function to work as intended generally, numbers having lesser orders of magnitude need to be multiplied by a factor large enough for the argument to arrive at ±16.720082053122, which is the smallest input to produce ±1 (respectively) to fourteen digits of accuracy. | As the absolute value of the input becomes large, the convergence is achieved at a point closer to zero. For the function to work as intended generally, numbers having lesser orders of magnitude need to be multiplied by a factor large enough for the argument to arrive at ±16.720082053122, which is the smallest input to produce ±1 (respectively) to fourteen digits of accuracy. | ||
| Line 41: | Line 41: | ||
The definition of the hyperbolic tangent is: | The definition of the hyperbolic tangent is: | ||
<math> | |||
\tanh{x}=\frac{e^x-e^{-x}}{e^x+e^{-x}}=\frac{e^{2x}-1}{e^{2x}+1} | \tanh{x}=\frac{e^x-e^{-x}}{e^x+e^{-x}}=\frac{e^{2x}-1}{e^{2x}+1} | ||
</math> | |||
= Related Commands = | = Related Commands = | ||
| Line 51: | Line 51: | ||
* [[TI-BASIC:Cosh|Cosh(]] | * [[TI-BASIC:Cosh|Cosh(]] | ||
* [[TI-BASIC:Arcosh|coshֿ¹(]] | * [[TI-BASIC:Arcosh|coshֿ¹(]] | ||
* [[TI-BASIC:Artanh|tanhֿ¹(]][[Category:TI-BASIC]] | * [[TI-BASIC:Artanh|tanhֿ¹(]] | ||
[[Category:TI-BASIC]] | |||
[[Category:TIBD]] | [[Category:TIBD]] | ||
Latest revision as of 19:15, 24 February 2016
Command Summary
Calculates the hyperbolic tangent of a value.
Command Syntax
tanh(value)
Menu Location
The tanh( command is only found in the Catalog. Press:
- 2nd CATALOG to access the command catalog.
- T to skip to commands starting with T.
- Scroll down and select tanh(.
TI-83/84/+/SE
1 byte
Calculates the hyperbolic tangent of a value. The hyperbolic trig functions Sinh(, Cosh(, and tanh( are an analog of normal trig functions, but for a hyperbola, rather than a circle. They can be expressed in terms of real powers of e, and don't depend on the Degree or Radian mode setting.
tanh(0)
0
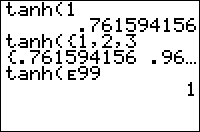
tanh(1)
.761594156
Like normal trig commands, tanh( works on lists as well, but not on complex numbers, even though the function is often extended to the complex numbers in mathematics.
Advanced Uses
The tanh( command can be used to approximate the sign function:
<math> \operatorname{sgn} x=\begin{cases}-1&\text{if }x<0,\\0&\text{if }x=0,\\1&\text{if }x>0.\end{cases} </math>
As the absolute value of the input becomes large, the convergence is achieved at a point closer to zero. For the function to work as intended generally, numbers having lesser orders of magnitude need to be multiplied by a factor large enough for the argument to arrive at ±16.720082053122, which is the smallest input to produce ±1 (respectively) to fourteen digits of accuracy.
5/12→X
.4166666667
tanh(E9X)
1
tanh(-E9X)
-1
Formulas
The definition of the hyperbolic tangent is: <math> \tanh{x}=\frac{e^x-e^{-x}}{e^x+e^{-x}}=\frac{e^{2x}-1}{e^{2x}+1} </math>