TI-BASIC:Det: Difference between revisions
Initial automated import |
KermMartian (talk | contribs) No edit summary |
||
| Line 21: | Line 21: | ||
For 2×2 matrices, the determinant is simply | For 2×2 matrices, the determinant is simply | ||
<math> | |||
\det\left( \begin{bmatrix} a & b\\c & d \end{bmatrix} \right) = \begin{vmatrix} a & b\\c & d \end{vmatrix} = ad-bc | \det\left( \begin{bmatrix} a & b\\c & d \end{bmatrix} \right) = \begin{vmatrix} a & b\\c & d \end{vmatrix} = ad-bc | ||
</math> | |||
For larger matrices, the determinant can be computed using the [wikipedia:Laplace_expansion Laplace expansion], which allows you to express the determinant of an n×n matrix in terms of the determinants of (n-1)×(n-1) matrices. However, since the Laplace expansion takes <math>O\left( n! \right)</math> operations, the method usually used in calculators is [http://mathworld.wolfram.com/GaussianElimination.html Gaussian elimination], which only needs <math>O\left( n^3 \right)</math> operations. | For larger matrices, the determinant can be computed using the [wikipedia:Laplace_expansion Laplace expansion], which allows you to express the determinant of an n×n matrix in terms of the determinants of (n-1)×(n-1) matrices. However, since the Laplace expansion takes <math>O\left( n! \right)</math> operations, the method usually used in calculators is [http://mathworld.wolfram.com/GaussianElimination.html Gaussian elimination], which only needs <math>O\left( n^3 \right)</math> operations. | ||
| Line 29: | Line 29: | ||
The matrix is first decomposed into a unit lower-triangular matrix and an upper-triangular matrix using elementary row operations: | The matrix is first decomposed into a unit lower-triangular matrix and an upper-triangular matrix using elementary row operations: | ||
<math> | |||
\begin{pmatrix}{1}&{}&{}\\ {\vdots}&{\ddots}&{}\\ {\times}&{\cdots}&{1}\end{pmatrix} | \begin{pmatrix}{1}&{}&{}\\ {\vdots}&{\ddots}&{}\\ {\times}&{\cdots}&{1}\end{pmatrix} | ||
\begin{pmatrix}{\times}&{\cdots}&{\times}\\ {}&{\ddots}&{\vdots}\\ {}&{}&{\times}\end{pmatrix} | \begin{pmatrix}{\times}&{\cdots}&{\times}\\ {}&{\ddots}&{\vdots}\\ {}&{}&{\times}\end{pmatrix} | ||
</math> | |||
The determinant is then calculated as the product of the diagonal elements of the upper-triangular matrix. | The determinant is then calculated as the product of the diagonal elements of the upper-triangular matrix. | ||
| Line 44: | Line 44: | ||
* [[TI-BASIC:Identity|Identity(]] | * [[TI-BASIC:Identity|Identity(]] | ||
* [[TI-BASIC:Ref|Ref(]] | * [[TI-BASIC:Ref|Ref(]] | ||
* [[TI-BASIC:Rref|Rref(]][[Category:TI-BASIC]] | * [[TI-BASIC:Rref|Rref(]] | ||
[[Category:TI-BASIC]] | |||
[[Category:TIBD]] | [[Category:TIBD]] | ||
Latest revision as of 19:13, 24 February 2016
Command Summary
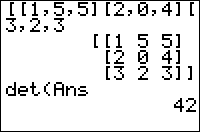
Calculates the determinant of a square matrix.
Command Syntax
det(matrix)
Menu Location
Press:
- MATRX (83) or 2nd MATRX (83+ or higher) to access the matrix menu
- LEFT to access the MATH submenu
- ENTER to select det(.
TI-83/84/+/SE
1 byte
The det( command calculates the determinant of a square matrix. If its argument is not a square matrix, ERR:INVALID DIM will be thrown.
Advanced Uses
If [A] is an N×N matrix, then the roots of det([A]-X identity(N)) are the eigenvalues of [A].
Formulas
For 2×2 matrices, the determinant is simply
<math> \det\left( \begin{bmatrix} a & b\\c & d \end{bmatrix} \right) = \begin{vmatrix} a & b\\c & d \end{vmatrix} = ad-bc </math>
For larger matrices, the determinant can be computed using the [wikipedia:Laplace_expansion Laplace expansion], which allows you to express the determinant of an n×n matrix in terms of the determinants of (n-1)×(n-1) matrices. However, since the Laplace expansion takes <math>O\left( n! \right)</math> operations, the method usually used in calculators is Gaussian elimination, which only needs <math>O\left( n^3 \right)</math> operations.
The matrix is first decomposed into a unit lower-triangular matrix and an upper-triangular matrix using elementary row operations:
<math> \begin{pmatrix}{1}&{}&{}\\ {\vdots}&{\ddots}&{}\\ {\times}&{\cdots}&{1}\end{pmatrix} \begin{pmatrix}{\times}&{\cdots}&{\times}\\ {}&{\ddots}&{\vdots}\\ {}&{}&{\times}\end{pmatrix} </math>
The determinant is then calculated as the product of the diagonal elements of the upper-triangular matrix.
Error Conditions
- ERR:INVALID DIM is thrown when the matrix is not square.