TI-BASIC:Radian Mode: Difference between revisions
Initial automated import |
Automated internal link correction |
||
| (One intermediate revision by the same user not shown) | |||
| Line 19: | Line 19: | ||
The input is differently interpreted: | The input is differently interpreted: | ||
* [[TI-BASIC: | * [[TI-BASIC:P_Rx|P►Rx(]], [[TI-BASIC:P►Ry(|P►Ry(]] | ||
* [[TI-BASIC:Sin|Sin(]], [[TI-BASIC:Cos|Cos(]], [[TI-BASIC:Tan|Tan(]] | * [[TI-BASIC:Sin|Sin(]], [[TI-BASIC:Cos|Cos(]], [[TI-BASIC:Tan|Tan(]] | ||
| Line 27: | Line 27: | ||
* [[TI-BASIC:Arcsin|sinֿ¹(]], [[TI-BASIC:Arccos|cosֿ¹(]], [[TI-BASIC:Arctan|tanֿ¹(]] | * [[TI-BASIC:Arcsin|sinֿ¹(]], [[TI-BASIC:Arccos|cosֿ¹(]], [[TI-BASIC:Arctan|tanֿ¹(]] | ||
* [[TI-BASIC:Polar_Display|►Polar]] (and complex numbers when in [[TI-BASIC:Re_Thetai|re^θi]] mode) | * [[TI-BASIC:Polar_Display|►Polar]] (and complex numbers when in [[TI-BASIC:Re_Thetai|re^θi]] mode) | ||
* | * <sup>[[TI-BASIC:Radian_Symbol|r]]</sup>, [[TI-BASIC:Degree_Symbol|°]] | ||
However, some commands are notably unaffected by angle mode, even though they involve angles, and this may cause confusion. This happens with the [[TI-BASIC:Sinreg|SinReg]] command, which assumes that the calculator is in Radian mode even when it's not. As a result, the regression model it generates will graph incorrectly in Degree mode. | However, some commands are notably unaffected by angle mode, even though they involve angles, and this may cause confusion. This happens with the [[TI-BASIC:Sinreg|SinReg]] command, which assumes that the calculator is in Radian mode even when it's not. As a result, the regression model it generates will graph incorrectly in Degree mode. | ||
| Line 45: | Line 45: | ||
= Optimization = | = Optimization = | ||
It's sometimes beneficial to use the | It's sometimes beneficial to use the <sup>[[TI-BASIC:Radian_Symbol|r]]</sup> command instead of switching to Radian mode. The <sup>r</sup> symbol will make sure a number is interpreted as a radian angle, even in degree mode, so that, for example: | ||
{{Template:TI-BASIC:Prgm-code | {{Template:TI-BASIC:Prgm-code | ||
| Line 53: | Line 53: | ||
sin(π) | sin(π) | ||
<span style="color:#F7F7F7;">..................</span>.0548036651 | <span style="color:#F7F7F7;">..................</span>.0548036651 | ||
sin(π | sin(π<sup>r</sup>) | ||
<span style="color:#F7F7F7;">..................</span>0|#F7F7F7;">..................</span>0]] | <span style="color:#F7F7F7;">..................</span>0|#F7F7F7;">..................</span>0]] | ||
| Line 62: | Line 62: | ||
* [[TI-BASIC:Degree_Mode|Degree]] | * [[TI-BASIC:Degree_Mode|Degree]] | ||
* | * <sup>[[TI-BASIC:Radian_Symbol|r]]</sup> | ||
* [[TI-BASIC:Degree_Symbol|°]][[Category:TI-BASIC]] | * [[TI-BASIC:Degree_Symbol|°]][[Category:TI-BASIC]] | ||
[[Category:TIBD]] | [[Category:TIBD]] | ||
Latest revision as of 23:54, 24 February 2016
Command Summary
Puts the calculator in Radian mode.
Command Syntax
Radian
Menu Location
While editing a program, press:
- MODE to access the mode menu.
- Use arrows and ENTER to select Radian.
TI-83/84/+/SE
1 byte
The Radian command puts the calculator into Radian mode, where the inputs and/or outputs to trig functions are assumed to be radian angles.
Angles measured in radians range from 0 to 2π. They are defined as the arc length of the arc, on a unit circle (circle with radius 1), that corresponds to the angle when it is placed in the center. This definition actually only differs from degree measurements by a constant factor.
To convert from a degree angle to a radian angle, multiply by 180/π. To go the other way, and get a radian angle from a degree angle, multiply by π/180.
The following commands are affected by whether the calculator is in Radian or Degree mode:
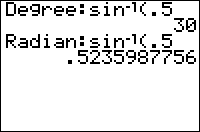
The input is differently interpreted:
The output is differently expressed:
However, some commands are notably unaffected by angle mode, even though they involve angles, and this may cause confusion. This happens with the SinReg command, which assumes that the calculator is in Radian mode even when it's not. As a result, the regression model it generates will graph incorrectly in Degree mode.
Also, complex numbers in polar form are an endless source of confusion. The angle( command, as well as the polar display format, are affected by angle mode. However, complex exponentials (see the e^( command), defined as <math>\definecolor{darkgreen}{rgb}{0.90,0.91,0.859}\pagecolor{darkgreen} e^{i\theta}=\cos\theta+i\sin\theta</math>, are evaluated as though in Radian mode, regardless of the angle mode. This gives mysterious results like the following:
Degree:re^θi Done e^(πi) 1e^(180i) Ans=e^(180i) 0 (false)
Overall, it's better to put your calculator in Radian mode when dealing with polar form of complex numbers, especially since no mathematician would ever use degrees for the purpose anyway.
Optimization
It's sometimes beneficial to use the r command instead of switching to Radian mode. The r symbol will make sure a number is interpreted as a radian angle, even in degree mode, so that, for example:
Template:TI-BASIC:Prgm-code..................[[TI-BASIC:/span>Done sin(π) ...................0548036651 sin(πr) ..................0|#F7F7F7;">..................0]]
This is smaller when only one trig calculation needs to be done. Also, it doesn't change the user's settings, which are good to preserve whenever possible.