TI-BASIC:Fnint: Difference between revisions
From Learn @ Cemetech
Jump to navigationJump to search
Initial automated import |
Automated superscript correction |
||
| Line 10: | Line 10: | ||
}} | }} | ||
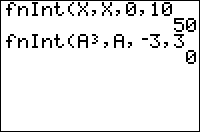
fnInt(''f''(''var''),''var'',''a'',''b''[,''tol'']) computes an approximation to the definite integral of ''f'' with respect to ''var'' from ''a'' to ''b''. ''tol'' controls the accuracy of the integral computed. The default value of ''tol'' is 10 | fnInt(''f''(''var''),''var'',''a'',''b''[,''tol'']) computes an approximation to the definite integral of ''f'' with respect to ''var'' from ''a'' to ''b''. ''tol'' controls the accuracy of the integral computed. The default value of ''tol'' is 10<sup>-5</sup>. fnInt( returns exact results for functions that are polynomials of small degree. | ||
fnInt( only works for real numbers and expressions. The [http://mathworld.wolfram.com/Gauss-KronrodQuadrature.html Gauss-Kronrod method] is used for approximating the integral. | fnInt( only works for real numbers and expressions. The [http://mathworld.wolfram.com/Gauss-KronrodQuadrature.html Gauss-Kronrod method] is used for approximating the integral. | ||
Latest revision as of 22:26, 24 February 2016
Command Summary
Approximately computes a definite integral.
Command Syntax
fnInt(f(var),var,a,b[,tol])
Menu Location
Press
- Press MATH to access the Math menu.
- 9 to select fnInt(, or use arrows.
TI-83/84/+/SE
1 byte
fnInt(f(var),var,a,b[,tol]) computes an approximation to the definite integral of f with respect to var from a to b. tol controls the accuracy of the integral computed. The default value of tol is 10-5. fnInt( returns exact results for functions that are polynomials of small degree.
fnInt( only works for real numbers and expressions. The Gauss-Kronrod method is used for approximating the integral.
Tip: Sometimes, to get an answer of acceptable accuracy out of fnInt(, substitution of variables and analytic manipulation may be needed.
fnInt(1/X,X,1,2) .6931471806 fnInt(ln(X),X,0,1) <a difficult example> -.999998347 fnInt(ln(X),X,0,1,e-11) -1
Error Conditions
- ERR:DOMAIN is thrown if tol is 0.
- ERR:ILLEGAL NEST is thrown if fnInt( occurs in the expression to be integrated.
- ERR:TOL NOT MET may occur if the tolerance is too small.