TI-BASIC:Sigmaint: Difference between revisions
Initial automated import |
Automated superscript correction |
||
| (One intermediate revision by one other user not shown) | |||
| Line 29: | Line 29: | ||
Now, we use the finance solver to solve for PMT. Since you intend to pay out the entire loan, FV is 0. Using either the interactive TVM solver, or the [[TI-BASIC:Tvm|tvm_Pmt]] command, we get a value of about -$733.76 for PMT. | Now, we use the finance solver to solve for PMT. Since you intend to pay out the entire loan, FV is 0. Using either the interactive TVM solver, or the [[TI-BASIC:Tvm|tvm_Pmt]] command, we get a value of about -$733.76 for PMT. | ||
We are ready to use ΣInt(. We are interested in the payments made during the first five years; that is, between the 1 | We are ready to use ΣInt(. We are interested in the payments made during the first five years; that is, between the 1<sup>st</sup> payment and the 5*12=60<sup>th</sup> payment. ΣInt(1,60) gives us the answer: -$39095.73 (the negative sign simply indicates the direction of cash flow) | ||
= Formulas = | = Formulas = | ||
| Line 35: | Line 35: | ||
ΣInt( is calculated in terms of [[TI-BASIC:Sigmaprn|ΣPrn(]], for which a recurrence exists. Since the total amount paid during an interval is known (it's the payment size, multiplied by the number of payments), we can subtract ΣPrn( from this total to get ΣInt(: | ΣInt( is calculated in terms of [[TI-BASIC:Sigmaprn|ΣPrn(]], for which a recurrence exists. Since the total amount paid during an interval is known (it's the payment size, multiplied by the number of payments), we can subtract ΣPrn( from this total to get ΣInt(: | ||
<math> | |||
\operatorname{\Sigma Int}(n_1,n_2)=(n_2-n_1+1)\operatorname{PMT}-\operatorname{\Sigma Prn}(n_1,n_2) | \operatorname{\Sigma Int}(n_1,n_2)=(n_2-n_1+1)\operatorname{PMT}-\operatorname{\Sigma Prn}(n_1,n_2) | ||
</math> | |||
= Error Conditions = | = Error Conditions = | ||
Latest revision as of 22:25, 24 February 2016
Command Summary
For an [wikipedia:Amortization_schedule amortization schedule], calculates the interest amount paid over a range of payments.
Command Syntax
ΣInt(paymentt1, payment2, [roundvalue])
Menu Location
On the TI-83, press:
- 2nd FINANCE to access the finance menu.
- ALPHA A to select ΣInt(, or use arrows and ENTER.
On the TI-83+ or higher, press:
- APPS to access the applications menu.
- 1 or ENTER to select Finance...
- ALPHA A to select ΣInt(, or use arrows and ENTER.
TI-83/84/+/SE
2 bytes
The ΣInt( command calculates, for an [wikipedia:Amortization_schedule amortization schedule], the interest over a range of payments: the portion of those payments that went toward paying interest. Its two required arguments are payment1 and payment2, which define the range of payments we're interested in. However, it also uses the values of the finance variables PV, PMT, and I% in its calculations.
The optional argument, roundvalue, is the number of digits to which the calculator will round all internal calculations. Since this rounding affects further steps, this isn't the same as using Round( to round the result of ΣInt( to the same number of digits.
Usually, you will know the values of N, PV, and I%, but not PMT. This means you'll have to use the finance solver to solve for PMT before calculating ΣInt(; virtually always, FV will equal 0.
Sample Problem
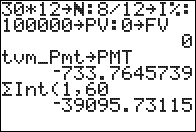
Imagine that you have taken out a 30-year fixed-rate mortgage. The loan amount is $100000, and the annual interest rate (APR) is 8%. Payments will be made monthly. How much of the amount that was paid in the first five years went towards interest?
We know the values of N, I%, and PV, though we still need to convert them to monthly values (since payments are made monthly). N is 30*12, and I% is 8/12. PV is just 100000.
Now, we use the finance solver to solve for PMT. Since you intend to pay out the entire loan, FV is 0. Using either the interactive TVM solver, or the tvm_Pmt command, we get a value of about -$733.76 for PMT.
We are ready to use ΣInt(. We are interested in the payments made during the first five years; that is, between the 1st payment and the 5*12=60th payment. ΣInt(1,60) gives us the answer: -$39095.73 (the negative sign simply indicates the direction of cash flow)
Formulas
ΣInt( is calculated in terms of ΣPrn(, for which a recurrence exists. Since the total amount paid during an interval is known (it's the payment size, multiplied by the number of payments), we can subtract ΣPrn( from this total to get ΣInt(:
<math> \operatorname{\Sigma Int}(n_1,n_2)=(n_2-n_1+1)\operatorname{PMT}-\operatorname{\Sigma Prn}(n_1,n_2) </math>
Error Conditions
- ERR:DOMAIN is thrown if either payment number is negative or a decimal.