TI-BASIC:1 Propzint: Difference between revisions
Initial automated import |
Automated @@ correction |
||
| Line 2: | Line 2: | ||
|picture=1-PROPZINT.GIF | |picture=1-PROPZINT.GIF | ||
|summary=Computes a Z confidence interval of a proportion. | |summary=Computes a Z confidence interval of a proportion. | ||
|syntax=1-PropZInt(''x'', ''n'' | |syntax=1-PropZInt(''x'', ''n''<nowiki>[</nowiki>, ''confidence level''<nowiki>]</nowiki>) | ||
|location=When editing a program, press: | |location=When editing a program, press: | ||
# STAT to access the statistics menu | # STAT to access the statistics menu | ||
Latest revision as of 21:39, 24 February 2016
Command Summary
Computes a Z confidence interval of a proportion.
Command Syntax
1-PropZInt(x, n[, confidence level])
Menu Location
When editing a program, press:
- STAT to access the statistics menu
- LEFT to access the TESTS submenu
- ALPHA A to select 1-PropZInt(, or use arrows
(this key sequence will give you the 1-PropZInt... screen outside a program)
TI-83/84/+/SE
2 bytes
The 1-PropZInt( command calculates a confidence interval for a proportion, at a specific confidence level: for example, if the confidence level is 95%, you are 95% certain that the proportion lies within the interval you get. The command assumes that the sample is large enough that the normal approximation to binomial distributions is valid: this is true if, in the sample you take, the positive and negative counts are both >5.
The 1-PropZInt( command takes 3 arguments. The first, x, is the positive count in the sample. The second, n, is the total size of the sample. (So the sample proportion is equal to x out of n). The third argument is the confidence level, which defaults to 95.
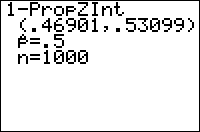
The output gives you a confidence interval of the form (a,b), meaning that the true proportion π is most likely in the range a<π<b, and the value of x/n.
Sample Problem
You want to know the proportion of students at your school that support a particular political candidate. You take a random sample of 50 students, and find that 22 of them support that candidate. 22, the positive count, and 50-22=28, the negative count, are both >5, so the assumption is satisfied.
Using 22 for x, and 50 for n, you decide to find a 95% confidence interval. The syntax for that is:
:1-PropZInt(22,50,95 which can also be :1-PropZInt(22,50,.95
The output if you run the above code will look approximately like this:
1-PropZInt (.30241,.57759) p=.44 n=50
This tells you that between about 30.2% and about 57.8% of the students at your school are in support of the political candidate.
Optimization
If the confidence level is 95%, you can omit the final 95, since that is the default value:
:1-PropZInt(22,50,95 can be :1-PropZInt(22,50
Error Conditions
- ERR:DOMAIN is thrown if the sample proportion is not between 0 and 1, any argument is negative, or the confidence level is 100 or more.